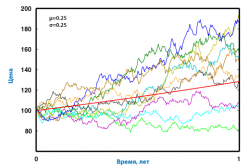
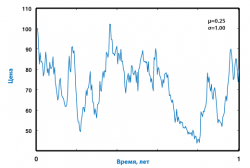
Вспомните уроки физики. Что характерно для этой науки? Для любого физического явления есть строгая математическая модель его развития в пространстве и времени. Ценность таких моделей не подлежит сомнению, поскольку они не только делают более понятной картину нашего мира, но и позволяют прогнозировать его будущее состояние. Финансовые рынки также являются частью реальности, причем эта реальность по большей части описывается цифрами: цена, объем, капитализация и т.п. – все это количественные характеристики. Раз так, напрашивается вопрос: возможно ли хотя бы приблизительно описать динамику рынка при помощи какой-либо математической модели? Ответ на него – положительный, и с одной из простейших таких моделей мы познакомимся в этой статье.

В современной экономике широко применяются методы математического моделирования. Возникла даже отрасль знаний под названием «эконофизика». Эконофизики пытаются описывать экономические явления при помощи физических методов и моделей. Одной из популярных таких моделей является геометрическое броуновское движение, так же известное под именем экспоненциального броуновского движения. Эта модель может достаточно успешно применяться для моделирования ценовой динамики рисковых активов – таких как акции, фондовые индексы, товарные фьючерсы и т.п. В частности она используется в теории портфельной оптимизации (оптимизация структуры и размера торговой позиции) и опционного ценообразования (т.н. модель Блэка-Шоулза).

Локальная динамика

Введем основные обозначения: S_t – цена акции в некоторый момент времени t, µ (мю) – доходность, σ (сигма) – волатильность, W_t – значение случайного процесса в момент t, источник «шума». Тогда модель геометрического броуновского движения можно записать следующим образом:

dS_t = µS_tdt + σS_tdW_t (1)

Что стоит за всеми этими обозначениями? Символы dt и dS_t обозначают приращения времени и цены. Если принять за единицу времени один финансовый год, dt может быть, напр., одним торговым днем, что примерно составляет 1/250, т.е. dt = 0.004. dS_t – это приращение (изменение) цены акции за момент времени dt. Напр., если на начало какого-то дня акция стоила $100, а на конец $101, это означает что dS_t = $101-$100 = $1. Если бы акция упала до $99 к концу дня, dS_t = $99-$100 = -$1. Таким образом, dS_t – это просто денежное изменение стоимости акции за момент времени dt, напр., за один торговый день.

Давайте пока отбросим самый непонятый кусочек формулы σS_tdW_t и сосредоточимся на следующем выражении: dS_t = µS_tdt. Чтобы стало яснее, зададим конкретные числовые значения всем параметрам. Пускай в начальный момент времени t = 0 акция стоит $100: S₀ = $100. Средняя доходность составляет µ = 0.25 (25% годовых). Приращение времени – один торговый день (1/250 торгового года) dt = 0.004. В итоге имеем:

dS₀ = µS₀dt = 0.25 x $100 x 0.004 = $0.1

Это означает, что ожидаемое изменение цены акции к концу торгового дня составляет 10 центов. Таким образом, согласно модели к концу дня акция будет стоить S₀ + dS₀ = $100 + $0.1 = $100.1. Повторив процедуру, мы можем вычислить ожидаемое значение цены акции еще на шаг вперед. Для этого сначала найдем приращение на момент t=0.004 (второй торговый день): 0.25 x $100.1 x 0.004 = $0.1001 (в формулу просто подставляется вычисленное на предыдущем шаге ожидаемое значение цены – $100.1). Следовательно на конец второго дня имеем ожидаемое значение цены S_0.004 + dS_0.004 = $100.1 + $0.1001 = $100.2001. Стоит отметить, что на втором шаге цена выросла чуть больше – на 10.01 цента.

Продолжая вычисления аналогичным образом, можно найти ожидаемую цену акции в любой желаемый момент времени. По мере роста цены, ее ожидаемый прирост также будет расти. Напр., к тому моменту, когда акция дорастет до $200, согласно модели, дневной прирост цены составит уже 0.25 x $200 x 0.004 = $0.2, или 20 центов. Это является очень логичным, поскольку инвесторы требуют от ценной бумаги не абсолютный, а процентный доход. Имея капитал в $200, нет никакой разницы, купить две акции компании ABC по $100 за долю или одну акцию компании XYZ за $200. Если инвестиционное сообщество одинаково оценивает перспективы этих бумаг, обе они будут иметь одинаковую ожидаемую процентную доходность, независящую от текущей цены акции, и значит, при текущем уровне цен первая акция будет прирастать на 10 центов, а вторая на 20 центов в день. Учитывая эти соображения, исходную формулу можно переписать в другом виде, разделив на S_t:

dS_t/S_t = µdt + σdW_t (2)

В такой записи становится понятным, что ожидаемая процентная доходность за момент времени dt не зависит от текущего ценового уровня S_t и является постоянной величиной – µ. В нашем примере она равна 25% годовых.

Добавим шума

Давайте теперь обратимся ко второму слагаемому формулы σS_tdW_t. Поскольку цены реальных финансовых активов демонстрируют весьма хаотичную динамику, что визуально выражается в «изрезанности» ценового графика, его «негладкости», в модели обязательно должен быть источник шума. Здесь им выступает dW_t. Что это такое? Это приращение т.н. «процесса Винера» за время dt. Более подробно можно расписать так: dW_t = ε_tdt^½, где ε – случайная величина со стандартным нормальным распределением. Нормальное распределение – это одно из элементарных вероятностных распределений. Визуально оно напоминает колокол, центрированный в точке среднего значения. Это означает, что большие отклонения от среднего менее вероятны, чем малые, что согласуется с практикой и здравым смыслом. Стандартное нормальное распределение имеет нулевое среднее значение и единичное стандартное отклонение (волатильность). Итак, dW_t – это приращение стандартной нормальной величины за момент времени dt. Какие характеристики имеет это приращение? Среднее значение его также равно нулю, а вот волатильность, согласно правилам теории вероятностей будет dt^½, то есть корню из времени. В нашем случае dt^½ = sqrt(0.004) ≈ 0.0632. Если теперь вернуться к первому шагу вычислений, то согласно полной формуле ожидаемый прирост цены в начальный период времени будет равен:

dS₀ = µS₀dt + σS₀dW₀ = 0.25 x $100 x 0.004 + 0.25 х $100 x dW₀ = $0.1 + $25 x dW₀

Таким образом, приращение цены в начальный момент времени можно выразить как сумму его ожидаемого значения и случайной составляющей – $25 x dW₀. Волатильность dW_t нам известна, поэтому можно найти волатильность случайной компоненты в момент времени t=0. Она будет примерно равна 0.0632 x 0.25 х $100 = $1.58. Иными словами, при цене акции $100 типичное дневное изменение будет равно $0.1 ± $1.58. Величина $1.58 – это среднее типичное колебание случайной компоненты в модели. На практике в какие-то дни оно может быть больше, а в какие-то меньше, но в среднем будет колебаться на эту величину, а согласно «правилу трех сигм» почти всегда не будет превышать $1.58 x 3 = $4.74. По мере роста цены волатильность приращений, как и их доходность, будет расти. Волатильность же процентной доходности будет величиной постоянной. В нашем случае – 25% годовых или 1.58% в день (0.25 x 0.0632 x 100%).

Непрерывное время

Итак, мы имеем модель локальной динамики цены, позволяющую вычислить ожидаемую величину изменения цены на шаг вперед от текущего момента времени, а также включающую и случайную компоненту. Настало время более пристально изучить элемент dt. До сих пор мы полагали, что это один торговый день, примерно равный 1/250 торгового года. На самом деле, согласно теоретической спецификации модели dt – это сколь угодно малый промежуток времени. Представьте себе какой-нибудь маленький временной интервал. Если вам на ум пришла миллисекунда, dt меньше миллисекунды. Он меньше любого временного интервала, который вы можете себе придумать или воспринять. Можно сказать, что dt – это одно «мгновение» времени или «миг». Это означает, что согласно модели геометрического броуновского движения цена может изменяться непрерывно, в любой мыслимый момент времени, причем без прыжков. Напр., если в какой-то момент времени акция стоила $100, а потом стала стоить $102, значит, согласно модели, непременно в какой-то промежуточный миг она стоила и $101, т.е. изменялась без прыжков. Это вступает в противоречие с практикой, поскольку нам известно, что цены активов изменяются скачкообразно. Однако противоречие не столь уж и велико, поскольку большую часть времени скачки имеют малую величину, скажем, 1-2 пункта. Кроме того, скачок может произойти в любой момент времени (минутные графики – это идеализация, порожденная нашим стремлением к упорядочиванию). В этом смысле модель согласуется с практикой, поскольку допускает изменение цены в любой мыслимый момент времени, а не строго «по расписанию», значит, можно сказать (хоть это и не совсем корректно), что модель геометрического броуновского движения – это модель тиковой динамики, т.е. она возникает на самом «молекулярном» уровне ценовых движений (тиковые графики). Это означает, что µ и σ являются мгновенными доходностью и волатильностью, выраженными в % годовых.

Экспоненциальный рост

Формула (1) на научном языке называется стохастическим дифференциальным уравнением. От обычного «диффура», изучаемого в классическом матане, оно отличается наличием случайной (стохастической компоненты) W_t. Как уже говорилось выше, действуя пошагово, можно вычислить ожидаемую цену не только в локальный момент времени, но и в любой более далекий период. Однако, поскольку dt – сколь угодно малый миг времени, придется проделать сколь угодно большое количество таких шагов. Математически это сводится к взятию интеграла, но не обычного, а стохастического. Такие интегралы имеют свои тонкости. Не вдаваясь в подробности, можно сказать, что уравнение (1) имеет решение, и оно имеет следующий вид:

S_t = S₀exp[(µ - ½σ²)t + σW_t] (3)

Это та же самая (1) модель динамики, только записанная в интегральной форме. Она позволяет легко найти ожидаемое значение цены в любой момент времени. Для этого нужно лишь задать стартовое значение цены S₀ и знать ожидаемые доходность и волатильность. Запись exp(x) обозначает экспоненциальную функцию. Она может быть также записана в другой форме: exp(x) = e^x ≈ 2.72^x. Формула (3) позволяет понять природу роста цены: цена рискового актива растет экспоненциально, т.е. со все более увеличивающейся скоростью. Выражение exp[µ - ½σ²] – это средняя геометрическая доходность (рост) акции. Если для простоты отбросить случайный член, модель роста можно записать через среднее геометрическое (G) как S_t = S₀G^t. Такая динамика цены соответствует модели сложного процента для безрискового актива (облигации или банковского счета), когда проценты начисляются на проценты, и это происходит непрерывно (на практике – очень часто, скажем, раз в день). Однако модель для акции в отличие от случая безрисковой облигации содержит в себе случайную компоненту σW_t. Она задает то, насколько «ухабистым» будет путь акции на дороге роста. Разыгрывая различные значения W_t, напр., при помощи генератора случайных чисел, можно получить целое семейство возможных траекторий движения цены. Волатильность W_t в момент времени t равна t^½, поэтому траектории, в начале стартующие из одной точки, со временем все больше и больше расползаются (см. картинку ниже). Это происходит из-за того, что у процесса геометрического броуновского движения нет памяти или механизма возвращающего цену к средним значениям. Геометрическое броуновское движение по смыслу соответствует дискретному процессу «случайного блуждания». Оно является его прямым аналогом в непрерывном времени. В физике похожее поведение демонстрируют молекулы – отсюда и название броуновское движение.

Риск-премия

Еще одна интересная особенность экспоненциального роста, заметная при записи в интегральной форме (3), заключается в том, что рост завит не только от средней доходности (µ), но и от волатильности (σ). Большие значения волатильности могут «убить» рост даже при положительной доходности. Этот факт на практике проявляется в том, что средняя арифметическая доходность всегда больше средней чистой геометрической доходности (G-1). Это означает также и то, что при одинаковой средней арифметической доходности рисковый актив всегда будет расти медленнее, чем безрисковая облигация, поскольку у облигации волатильность равна нулю. Поэтому рациональный инвестор, покупая рисковую бумагу, всегда требует премию за риск. Таким образом, для рационального инвестора акция представляет интерес, только если она имеет ожидаемую среднюю арифметическую доходность выше величины r + ½σ², где r – безрисковая ставка. При таком значении µ акция будет расти со скоростью безрисковой облигации, правда, при этом иметь не гладкую, а «ухабистую» траекторию (иметь просадки). Величина ½σ² является премией за риск. Следует отметить, что акция может представлять интерес и при меньших значениях риск-премии, когда она растет медленнее облигации, но не сама по себе, а как часть оптимального портфеля из акции и облигации.

Резюме

Подведем итоги нашего знакомства с геометрическим броуновским движением:

1. Геометрическое броуновское движение является простейшей моделью динамики цены рискового актива, описывая ее при помощи двух параметров – доходности и волатильности. Эта простота позволяет эффективно использовать ее при решении важных практических задач, таких как определение справедливой цены опциона или вычисление вероятности разорения/просадки. Используя эту модель, вероятности многих ценовых событий можно рассчитать при помощи довольно простых формул, даже не прибегая к методу статистических испытаний (Монте-Карло).

2. Модель близка к реальности в том, что допускает изменение цены в любой мыслимый момент времени. Модель расходится с реальностью, поскольку предполагает непрерывное (без скачков) изменение цены. Поэтому геометрическое броуновское движение лучше подходит для описания динамики высоколиквидных активов: «голубых фишек», индексов, основных валют. Тем не менее, в качестве первого приближения ее можно использовать и для менее ликвидных бумаг.

3. Геометрическое броуновское движение предполагает экспоненциальный рост, аналогичный росту капитала на банковском счете при частом начислении сложных процентов. Однако в отличие от банковского счета в модель включен источник шума – стандартная нормальная случайная величина. Наличие шума замедляет рост, а при высокой волатильности может даже полностью его уничтожить.

4. Геометрическое броуновское движение полезно не столько для прогноза будущей цены, сколько для общего понимания ценовой динамики и быстрой прикидки тех или иных вероятностей. Полезность модели для прогнозирования целиком зависит о точности оценок параметров – доходности и волатильности. На практике необходимо сначала спрогнозировать эти параметры на основе какого-либо статистического метода или фундаментального анализа, а уже потом подставлять в модельное уравнение. Если полученные оценки окажутся близкими к реальности (к неизвестным будущим µ и σ), геометрическое броуновское движение будет давать хорошие прогнозы.

© q-trader

[обсудить на форуме]