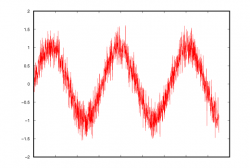
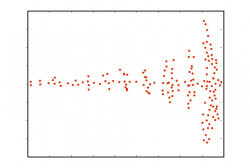
До сих пор мы рассматривали случайные величины изолированно. На практике многих инвесторов интересуют зависимости между различными финансовыми временными рядами. Особенно это актуально в прогнозировании и формировании портфеля. В этой лекции мы узнаем, что такое статистическая зависимость, познакомимся с простейшими инструментами ее измерения и моделирования – корреляционным и регрессионным анализом, а также заглянем и чуть дальше…

Статистическая зависимость

Поиск зависимостей и закономерностей между явлениями и процессами – одна из основных задач для любой науки. Особенно ярко зависимости проявляются в точных науках, таких как, напр., физика. Многие физические зависимости можно представить в виде графика некоторой функции: x², sin(x), ln(x) и т.п. Совсем другая картина наблюдается в науках экономических. В экономике тоже есть свои закономерности, но они, как правило, нестрогие – это не функции, а скорее тенденции или, как любят говорить трейдеры, – тренды. Часто статистическая зависимость представляет собой функциональную, на которую наложен некоторый «шум». Ниже приводится график такой зашумленной синусоиды:

Однако могут встречаться и более экзотические формы статистической зависимости. Так, на следующем графике отсутствует какая-либо выраженная тенденция по типу зашумленной функции, но можно заметить, что величины не являются полностью независимыми, поскольку с ростом x увеличивается волатильность y, что позволяет констатировать наличие статистической зависимости.

В теории вероятностей есть строгое определение независимости случайных величин. Случайные величины являются независимыми, если их совместная плотность вероятности равна произведению индивидуальных плотностей. В этом легко убедится на простом примере с монетой: вероятность выпадения двух решек подряд равна ¼ (½ × ½), поскольку эти события независимы и их индивидуальные вероятности равны ½.

Важность линейных зависимостей

Потенциально существует бесчисленное количество всевозможных зависимостей. Однако на практике, как правило, нет никаких оснований предполагать, что между изучаемыми финансовыми переменными существует какая-либо причудливая зависимость. Используя достаточно сложную функцию, мы легко можем подогнать какую-либо кривую, которая бы точно совпадала с точками имеющихся данных. Однако такая кривая будет явной фикцией, поскольку она будет подогнана ко всем шумам, содержащимся в выборке. Это явление получило название «переподгонка». В большинстве случаев уровень шума настолько высок, а наши априорные знания настолько низки, что максимум, на что мы можем претендовать – это идентификация линейной зависимости между переменными. Такой зависимости соответствует график прямой с некоторым наклоном (β) и смещением (α) относительно оси y. В общем случае с n объясняющими переменными это будет некоторая гиперплоскость. Мы уже не сможем ее визуализировать на графике, но, в принципе, это тоже очень простой объект.

Корреляционный анализ

Основным инструментом анализа линейных зависимостей является корреляционный анализ. Слово «корреляция» стало довольно расхожим среди инвесторов. Часто оно является синонимом понятия «зависимость». Так, в финансовых СМИ можно прочитать статью, в которой говорится, что фондовый рынок и нефть «коррелируют». Как правило, это означает всего лишь, что автор статьи предполагает наличие какой-то зависимости между ними. В математической статистике понятие «корреляция» применятся только к линейной зависимости: если какие-то величины некоррелированны, это означает лишь, что между ними отсутствует линейная зависимость, но может присутствовать более экзотическая взаимосвязь, напр., как на втором графике в этой лекции. Единственным исключением, для которого некоррелированность тождественна независимости является многомерное нормальное распределение. О нем мы поговорим чуть позже.

Коэффициент корреляции ρ является удобным инструментом анализа, поскольку он изменяется в диапазоне -1 … +1. В случае |ρ| = 1 имеется функциональная линейная зависимость величин. В промежуточных вариантах – линейная зависимость с шумом. При ρ = 0 в данных полностью доминирует шум, и зависимость отсутствует.

Коэффициент корреляции можно вычислить по следующей формуле:

_N

ⁱ⁼¹

где µ – средние значения переменных x и y, σ – их стандартные отклонения.

То есть, нужно найти матожидание произведения отклонений от средних и разделить их на произведение стандартных отклонений. Если не делить на σ_xσ_y, получается тоже важная для практики статистика, которая называется ковариацией.

В общем случае, когда изучаемых переменных больше чем две, коэффициент корреляции можно вычислить попарно для каждой из них. Полученная таблица называется корреляционной матрицей. Ниже приводится пример такой матрицы для трех величин:

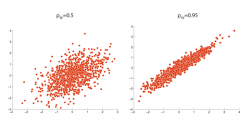
Можно отметить, что наиболее сильная зависимость (0.75) наблюдается между x и z. Также x слабо (0.25) коррелирует с y. А вот y и z – некоррелированы.

Интересным является вопрос о том, какую корреляцию следует считать сильной. Наивный ход мыслей приводит к выводу – большую 0.5. Это не так. Дело в том, что сила корреляции измеряется ее квадратом, который получил название коэффициента детерминации. Так, коэффициент детерминации равный 0.5 означает, что половина изменчивости y объясняется изменчивостью x. Этому соответствует коэффициент корреляции равный 0.5^½ ≈ 0.71. При ρ = 0.5 лишь четверть изменчивости y объясняется x, что вряд ли можно считать сильной связью. Таким образом, сильная корреляция должна быть больше 0.71.

Простая регрессия

Корреляции хороши для аналитических целей – изучения общей структуры зависимостей активов. Когда необходимо построить прогноз величины y по известному значению x, следует использовать регрессию. Регрессионный анализ позволяет выразить зависимость между переменными в виде:

y = α + β x,

что представляет собой наилучший линейный прогноз. Коэффициенты бета и альфа в уравнении регрессии легко вычислить, зная средние (µ), волатильности (σ) и корреляцию (ρ).

β = ρ_xy σ_y/σ_x

α = µ_y - βµ_x

Очень популярной является т.н. «рыночная модель». В качестве объясняющей переменной в этой модели выступает доходность рыночного индекса, такого как, напр., S&P 500, а в качестве объясняемой доходность по отдельной бумаге. Предположим, что мы на исторических данных получили следующие оценки параметров: волатильность акции σ_y = 50%, волатильность индекса σ_x = 25%, корреляция доходностей акции и индекса ρ_xy = 0.75, средняя доходность акции µ_y = 50%, средняя доходность индекса µ_x = 25%.

Найдем коэффициент бета: 0.75×50%×25% = 1.5. Альфа: 50% - 1.5×25% = 12.5%.

В итоге модель для доходностей акции (r_S) можно записать так:

r_S = 12.5% + 1.5 r_M

Так, если ожидаемая доходность по рыночному индексу составляет 40%, согласно модели ожидаемая доходность акции должна быть: 12.5% + 1.5×40% = 72.5%.

Интересно, что и при нулевой ожидаемой доходности рынка акция имеет положительную доходность равную коэффициенту альфа. В модели оценки капитальных активов CAPM доказывается, что в равновесной ситуации альфа должна быть равна безрисковой ставке r_f. Кроме того, размер β говорит о том, что наша акция относится к разряду «агрессивных», поскольку она, как правило, движется в полтора раза сильнее рынка.

Множественная регрессия

Когда число объясняющих переменных в модели регрессии больше одной, ее называют множественной регрессией. На практике множественную регрессию проще трактовать в терминах векторов и матриц. В математике эти объекты изучаются в рамках линейной алгебры. Знать ее начала неплохо, но не обязательно. Матрицы полезны тем, что позволяют существенно упростить обозначения и оперировать сложными многомерными объектами как обычными числами – скалярами. В матричных обозначениях модель регрессии можно записать так:

y = α + β’x,

где x = [x₁, x₂, … , x_n]’ – вектор значений объясняющих переменных, β = [β₁, β₂, … , β_n]’ – вектор коэффициентов бета.

Эта формула является сжатым представлением более развернутой записи:

y = α + β₁x₁ + β₂x₂ + … + β_nx_n

Решение для коэффициентов множественной регрессии в матричной форме записывается так:

β = Σ_x^-1σ_xy

α = µ_y - β’µ_x

Σ_x – ковариационная матрица объясняющих переменных, σ_xy – вектор-столбец ковариаций объясняющих переменных с объясняемой. Иногда их еще называют матрицей автоковариаций и вектором кроссковариаций соответственно. Символ ^-1 здесь означает обратную матрицу – обобщение понятия обратного числа: напр., 0.1 (1/10) – число обратное к 10. Символ «’» - это знак транспонирования. Транспонирование – это операция, превращающая вектор-столбец в вектор-строку, и наоборот. Обычно по умолчанию считается, что вектор – это столбец значений, поэтому запись вида x’задает вектор-строку. µ_x – вектор-столбец средних значений объясняющих переменных.

Эти формулы являются прямым обобщением простой одномерной регрессии. На практике их можно применять в специальном софте, особенно удобно – в MATLAB.

Корреляция и ковариация

Вектор коэффициентов бета рассчитывается через ковариационную матрицу. Она не очень удобна для понимания, поскольку зависит от единиц измерения величин. Для восприятия удобнее корреляционная матрица и вектор волатильностей. Эти объекты опытный эксперт может даже вывести «из головы», опираясь на собственный опыт и понимание структуры рынка, не прибегая к непосредственным измерениям. (На практике экспертные оценки, как правило, смешиваются с эмпирическими данными – байесовский подход к оцениванию параметров.) В таких ситуациях будет полезна формула, позволяющая получить ковариационную матрицу через корреляционную матрицу и вектор волатильностей. В одномерном случае:

σ_xy = ρ_xyσ_xσ_y

В многомерном:

Σ = diag(σ) Ρ diag(σ)

Ρ – корреляционная матрица, diag(σ) – диагональная матрица, на главной диагонали которой стоят волатильности активов.

Тонкости уравнения регрессии

Давайте присмотримся более пристально к формуле для бета-коэффициента:

β = ρ_xy σ_y/σ_x

Наклон линии регрессии зависит от соотношения волатильностей объясняемой и объясняющей переменных и их корреляции. Беты большие единицы возникают при сильных корреляциях и различиях в уровнях волатильности. Если же корреляция отсутствует, β будет равна нулю, независимо от уровней волатильности. Не все беты сопоставимы между собой. Этим статистическая линейная модель зависимости отличается от функциональной. Если какой-то актив имеет β_A = 2 с рыночным индексом, а другой β_B = 1, не совсем корректно говорить о том, что у них разная чувствительность к рыночным движениям. Допустим, волатильность рынка σ_M = 25%, волатильности акций σ_A = 100% и σ_B = 33.33%, корреляции с индексом ρ_AM = 0.5 и ρ_BM = 0.75 соответственно. Если подставить эти цифры в формулу для бета-коэффициента, получим β_A = 2 и β_B = 1. Первая акция с β_A = 2 вроде бы сильнее реагирует на движения рынка, но у нее значительно ниже коэффициент корреляции с рынком ρ_AM = 0.5 по сравнению со второй. Большое значение β_A связано в основном с высоким уровнем волатильности этой бумаги, а не с силой корреляции. По этой причине бета-коэффициенты данных бумаг несопоставимы. Динамика второй акции значительно лучше предсказуема по динамике рынка. При сопоставлении бета-коэффициентов каких-либо бумаг, портфелей или инвестфондов, всегда следует обращать внимание на коэффициенты корреляции и детерминации, чтобы не оказаться в ситуации, когда вы сравниваете «огурцы с помидорами».

Уравнение регрессии также можно записать и через матожидания. В этом случае оно принимает вид:

µ_y|x = µ_y + β(x - µ_x),

где µ_y|x – условное матожидание y по x. Такой вариант записи позволяет взглянуть на линейную регрессию с еще одного угла зрения. Получается, что условное матожидание объясняемой переменной y равняется ее безусловному матожиданию (µ_y) плюс отклонению объясняющей переменной x от ее матожидания (µ_x), умноженному на коэффициент β. Отсюда следует, что нетривиальный прогноз возникает лишь в том случае, когда x отклоняется достаточно сильно от своего среднего значения (µ_x). Если же значение x=µ_x, наилучшим прогнозом y при этом условии является его безусловное среднее значение µ_y. Точно такая же ситуация возникает и при β=0.

За пределами корреляций

Рассмотренные нами в этой лекции корреляционные и ковариационные матрицы являются простейшими объектами, задающими зависимости на множестве активов. Фактически матрицы фиксируют только парные зависимости вида: x↔y, x↔z, y↔z. Можно ли утверждать, что попарно независимые величины полностью независимы? Это справедливо только для многомерного нормального закона распределения. Такой закон полностью определяется вектором средних значений µ и ковариационной матрицей Σ. Именно для него наиболее корректны корреляционный и регрессионный анализы. К сожалению, фондовый и другие рынки только приближенно описываются моделью многомерного нормального распределения, поэтому следует сказать несколько слов и о более сложных формах зависимости.

Для простоты представим, что рынок состоит только из трех активов, которые можно понимать, напр. как три секторных фонда, допустим, промышленный, финансовый и технологический. Предположим, что все эти три «бумаги» попарно некоррелированы. Как в таком случае можно представить более сложную зависимость между ними? Вспомним, что ковариация представляет собой матожидание произведения случайных величин (для простоты, пускай, здесь они будут с нулевыми средними значениями) или, как еще говорят, совместный момент второго порядка. Продолжая, эту аналогию можно вычислить моменты третьего порядка. Это уже будут матожидания произведений трех случайных величин (в т.ч. и ее произведений с самой собой). Структурно таким тройным зависимостям соответствует уже не матрица, а тензор (3-мерный). Если представить матрицу как квадратную решетку для хранения куриных яиц, то тензор уже будет столбиком из таких решеток, поставленных друг на друга, т.е. кубом. Каждое «яйцо» в этом столбике будет соответствовать определенному моменту 3-го порядка, напр.: <xxx>, <xyx>, <xyz> и так для всех комбинаций. Косые скобки здесь означают матожидание. У многомерного нормального закона все моменты высших порядков равны нулю. Это означает отсутствие более сложных, чем попарная, зависимостей.

Тензоры – это формальный способ описания и фиксации многомерных зависимостей, но, что на практике означают эти зависимости? Вернемся к нашему примеру с тремя некоррелированными фондами. Примером зависимости, возникающей в тройке активов, будет ситуация общего рыночного краха, когда проявляется тенденция к совместному падению цен всех трех активов. Получается, что в «нормальном» режиме активы могут быть попарно некоррелированны, а в экстремальных ситуациях, когда падает общий спрос на рисковые активы, «коррелированны» в смысле отличия от нуля <xyz>, т.е. совместное падение всех трех активов будет наблюдаться гораздо чаще, чем, если бы они были полностью независимыми. Этот пример можно расширить и на большее число активов. В общем случае зависимости могут наблюдаться между произвольными группами активов: тройками, четверками, пятерками и т.д.

Выводы

В заключении хотелось бы подвести итоги, а также обозначить практическую ценность изученных нами формул. Мы узнали, что такое функциональная, регрессионная и статистическая зависимость. Статистическая зависимость является наиболее общей. Линейная регрессионная зависимость является ее частным случаем и выражается в том, что при варьировании переменной x меняется условное матожидание y. Корреляционный и регрессионный анализ, по сути, очень похожи. Различие заключается в том, что корреляционный анализ проводится на корреляционной матрице, в которую входят безразмерные, нормированные элементы, и он нацелен на объяснение и понимание структуры зависимостей активов, а регрессионный анализ требует использования ковариационной матрицы и претендует на прогнозирование величин. Линейный регрессионный анализ является простейшей прогностической моделью. Для вас он может стать первым шагом к пониманию и построению более сложных математических конструкций.

У кого-то может возникнуть вопрос: зачем знать формулы коэффициентов бета и альфа, если сейчас есть куча статистических пакетов, автоматически рассчитывающих линейную регрессию? Дело в том, что сама по себе линейная регрессия часто может быть неинтересна, но она может входить в качестве блока в какие-то другие модели. Напр., трейдер может написать собственный технический индикатор, который будет использовать, в том числе, и регрессию и т.п. В этом случае без знания формул никак не обойтись. Кроме того, человек знающий формулы лучше понимает саму суть модели, и, как правило, более корректно ее использует.

© q-trader

[обсудить на форуме]