| MATLAB – используем обобщенное нормальное распределение |
| 23.04.2012 09:00 |
|
Одной из особенностью реальных финансовых данных являются т.н. «толстые хвосты». Распределение доходностей многих активов демонстрирует высокую концентрацию частот у центральных значений и в «хвостах». Такое поведение сильно отличается от того, что предполагается в рамках модели нормального распределения – стандартного статистического инструмента в классических финансах. Однако проблема более точного моделирования реальных ценовых движений довольно легко решается за счет обращения к более широкому классу распределений, в частности, к обобщенному нормальному. Все же это решение было бы почти бесполезным без его «компьютеризации». К счастью, ее легко можно осуществить, воспользовавшись возможностями Matlab, в чем мы и убедимся в этом уроке. Обобщенное нормальное распределение Обобщенное нормальное распределение, также известное под именем обобщенного экспоненциального может использоваться для моделирования широкого спектра вероятностных явлений. Оно объединяет в себе такие, казалось бы, разные законы как равномерный, нормальный, Лапласа и др. В отличие от обычного нормального распределения обобщенное характеризуется тремя параметрами: µ, σ, τ. Параметр «мю» отвечает за положение максимума плотности вероятности на горизонтальной оси, «сигма» – задает типичный размах колебаний относительно максимума, а «тау» – контролирует толщину хвостов. Обобщенное нормальное распределение следует применять для моделирования логдоходностей финансового актива. Более подробную информацию по этому распределению вы можете найти в книге Булашева или в нашем курсе лекций. Целью данного урока является только презентация полезных функций для системы Matlab. Функции Matlab Командой Q-trading.ru было разработано несколько Matlab-функций для обобщенного нормального распределения, в частности:
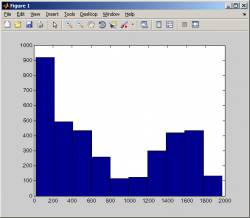
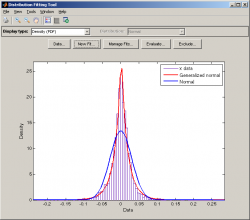
Кроме того, была разработана функция GND, позволяющая добавить обобщенное нормальное распределение в графический интерфейс подгонки Distribution Fitting Tool. Все эти файлы вы можете скачать в конце урока. Для того чтобы все корректно работало их следует поместить в текущий рабочий каталог – по умолчанию это папка «MATLAB» в «Моих документах». Ознакомиться с самим кодом можно открыв их в редакторе функций Matlab. Краткое описание функций gndpdf(x, µ, σ, τ) рассчитывает значение плотности вероятности в точке x. Она удобна для визуального ознакомления с вероятностным законом. Наложив ее на гистограмму эмпирических частот, можно увидеть, насколько хорошо они приближаются теоретической кривой. gndcdf(x, µ, σ, τ) позволяет найти вероятность того, что случайная величина x не превысит некоторое значение. gndinv(p, µ, σ, τ) позволяет найти значение x соответствующее некоторому вероятностному уровню p – квантиль, т.е. решает задачу обратную gndcdf(). gndCVaR(p, µ, σ, τ) позволяет вычислить среднее значение случайной величины ниже некоторого порогового значения соответствующего той или иной вероятности p. [PE, CI]=gndfit(x, p) рассчитывает значения оценок параметров методом максимального правдоподобия. gndrnd(µ, σ, τ, n, m) генерирует случайные числа из обобщенного нормального распределения. Пример: индекс ММВБ Чтобы стало понятнее, рассмотрим практический пример. Давайте подгоним обобщенное нормальное распределения к дневным логдоходностям индекса ММВБ. Получив оценки параметров, мы узнаем, как работают функции, и какую информацию на выходе они дают. Возьмем историю значений индекса ММВБ с 22 сентября 1997 года по конец 2011. Сохраним эти данные в Workspace под именем micex. Изучаемые нами в этом уроке функции следует применять к логдоходностям, а не к «ценам» индекса или любого другого актива с вероятностно похожей динамикой. Какая ерунда получается, если использовать цены, можно убедиться, построив гистограмму уровней индекса при помощи функции hist(micex) или через графический интерфейс: На картинке видно, что гистограмма уровней индекса имеет «шумовой» характер. Совсем другое дело – доходности. Их можно вычислить, воспользовавшись функцией x=price2ret(micex). Тем самым мы сохраняем их в памяти, обозначив как x, и потом легко можем обращаться к этому массиву данных. Далее, проследовав по меню Start/Toolboxes/Statistics/Distribution Fitting Tool, запустим графический интерфейс для подгонки распределений. В появившемся окошке выбираем File/Import Custom Distributions, отмечаем файл GND и нажимаем кнопку «Открыть». В списке доступных распределений должно появиться Generalized Normal*. Далее щелкаем по кнопке «Data…». Выбираем Data: x, нажимаем «Create Data Set» и закрываем это окно. В главном окне появится гистограмма доходностей по индексу ММВБ. На этот раз гистограмма демонстрирует четко проявляющуюся закономерность: максимальная концентрация частот наблюдается вблизи средних значений, минимальная – в хвостах, что согласуется со здравым смыслом, утверждающим, что 10% дневное движение цены – явление гораздо более редкое, чем, скажем, 1% движение. Теперь мы можем создавать подгонки различных распределений и изучать их качество. Нажимаем «New Fit…». Выбираем Distribution: Generalized normal и щелкаем «Apply». Внизу в поле «Result» появятся следующие цифры: Parameter Estimate mu 0.00176186 sigma 0.0280496 tau 0.860847 Из этих данных можно увидеть, что индекс ММВБ демонстрировал очень маленькую дневную доходность ≈0.18% и довольно высокую волатильность ≈2.8%. Параметр тау характеризует толщину хвостов и свидетельствует о значительном отклонении от обычного нормального закона – для него τ=2. Закроем окно и изучим точность подгонки визуально. Как видно из картинки, обобщенное нормальное распределение очень хорошо описывает реально наблюдавшийся разброс доходностей по индексу ММВБ. Для сравнения создадим новую подгонку – теперь уже для обычного нормального закона. Проделаем те же шаги, только выберем Distribution: Normal. На гистограмму будет наложена вторая, синяя линия нормального распределения. Очевидно, что даже наилучшим образом подогнанная эта кривая гораздо хуже моделирует реальные данные. Теперь, когда у нас есть оценки параметров, мы можем более содержательно поработать с функциями. Примечание: Для получения этих оценок можно было и не прибегать к визуальному интерфейсу, а использовать функцию [PE, CI]=gndfit(x, p), где PE – вектор оценок параметров, CI – матрица доверительных интервалов, p – уровень доверительной вероятности – эту переменную можно пропустить, тогда по умолчанию будет принят 5% уровень. Конструкцию [PE, CI] также можно пропустить – в этом случае gndfit() просто возвратит значение оценок параметров без доверительных интервалов. Плотность вероятности мы уже посмотрели в Distribution Fitting Tool, поэтому сразу обратимся к остальным функциям. Напр., можно задаться вопросом: какова вероятность индексу упасть более чем на 7% за день? Для этого используем: gndcdf(log(1-0.07),0.00176186,0.0280496,0.860847). Согласно нашей модели она составляет 1.31%. Значит, такие крупные обвалы цен не столь уж и редки. Для сравнения обычное нормальное распределение дает прогноз только 0.4%, т.е. оно значительно занижает риски сильных ценовых движений. Едем дальше. Каким может быть худший день в году? Для этого нам надо найти квантиль соответствующий вероятностному уровню 1/250 (250 примерное количество торговых дней в году), т.е. это %убыток, вероятность превышения которого 0.004. Пишем в командной строке: exp(gndinv(0.004,0.00176186,0.0280496,0.860847))-1. В итоге получаем худший день года – обвал более чем на 9.48%. На этом история не заканчивается. Можно вычислить еще и средний %убыток, возникающий при превышении этого порога: exp(gndCVaR(0.004,0.00176186,0.0280496,0.860847))-1. Ответ: 11.62%. Примечание: Несмотря на то, что обобщенное нормальное распределение предназначено для моделирования логдоходностей, его можно без труда приспособить и для обычных доходностей, c которыми мы реально и сталкиваемся при торговле, используя преобразования log() и exp(), что мы и проделали выше. Нам осталось рассмотреть только функцию для генерации случайных чисел. gndrnd(µ, σ, τ, n, 1) генерирует случайный вектор из n чисел, извлеченных из обобщенного нормального распределения. Для тренировки вы можете сгенерировать, напр., n=10000 выборочных значений, а потом через gndfit() оценить теоретические параметры, которые были заданы при генерации. Эти цифры должны быть очень близкими. Мы рассмотрели все функции. Оставшиеся gndstat() и k2t() имеют служебное значение – на них ссылаются другие функции. В частности, они используются для работы в визуальном интерфейсе подгонки (файл GND) и в gndfit(), поэтому все изученные нами выше функции должны храниться в одной рабочей директории Matlab – Current Folder. Функция k2t() рассчитывает параметр «тау» через показатель эксцесса выборочных данных и может использоваться при оценке параметров обобщенного нормального распределения методом моментов. Если для вычисления эксцесса вы используете матлабовскую функцию kurtosis(), то прежде чем подставить ее значение в k2t() из него следует вычесть 3, т.е. подставлять надо excess kurtosis. Итоги В этом уроке мы узнали как моделировать доходности финансовых активов при помощи обобщенного нормального распределения. Обобщенное нормальное распределение является весьма гибкой вероятностной моделью, позволяющей учитывать такие рыночные реалии как «толстые хвосты» и повышенную концентрацию частот у центра. Хотя это распределение не входит в стандартный набор Matlab, его легко можно интегрировать в систему при помощи пользовательских функций, что мы успешно и проделали. В дальнейшем вы можете свободно использовать эти функции для моделирования доходностей тех активов, которые вас интересуют, контроля рисков и т.п. © q-trader |

 Вход |
Вход | Регистрация
Регистрация


























 О проекте
О проекте Правовая информация
Правовая информация Напишите нам
Напишите нам Карта сайта
Карта сайта Новости
Новости Статьи
Статьи Рынки
Рынки Калькуляторы
Калькуляторы Софт
Софт Архив котировок
Архив котировок Индикаторы
Индикаторы Библиотека
Библиотека Словарь
Словарь Форум
Форум
Комментарии
q-trader
Руслан
EVVA
Харита
q-trader