| ОПБШ. Оценивание параметров |
| Автор: q-trader |
| 01.06.2015 09:42 |
|
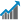
Ценность любой модели проявляется в ее практической реализуемости. Применительно к стохастическим процессам это предполагает возможность идентификации параметров по выборочным данным. Давайте рассмотрим, как это осуществить для обобщенного процесса Блэка-Шоулза. На первый взгляд обобщенный процесс Блэка-Шоулза не так уж сильно отличается от обычного. Однако появляющаяся здесь корреляция между доходностью и ценой сильно меняет дело в плане оценивания параметров. В частности сигма - важнейший параметр теперь выражается через условную дисперсию. Чтобы ее оценить, нужно строить регрессию ∆lnPt на lnPt - ∆t и t, т.е. вычислять линейную зависимость между текущей доходностью, предыдущей ценой и временем. Простейшим способом оценивания регрессии является т.н. "метод наименьших квадратов" (МНК). Как уже говорилось, дискретная версия ОПБШ выглядит следующим образом: lnPt = lnP + μt + (lnPt - ∆t - lnP - μ(t - ∆t))exp(-γ∆t) + N(½σ2(1 - exp(-2γ∆t))/γ). По сути это обычное уравнение регрессии с параметрами: α = lnP(1 - exp(-γ∆t)) + exp(-γ∆t)μ∆t, β = exp(-γ∆t), θ = μ(1 - exp(-γ∆t)), ε2 = ½σ2(1 - exp(-2γ∆t))/γ), т.е. lnPt = α + βlnPt - ∆t + θt + εt, выборочные оценки которого можно получить, например, обычным МНК. Параметр β определяет чувствительность к предыдущей цене, а θ - к времени. Таким образом, это обычная двухмерная регрессия. Используя данные зависимости, нетрудно выразить значения искомых параметров: γ = -lnβ/∆t, μ = θ/(1 - β), lnP = α/(1 - β) - θβ/(1 - β)2∆t, σ2 = -2ε2lnβ/(1 - β2)/∆t. Остается лишь воплотить все это в виде кода. Обозначив g = γ, m = μ, s = σ, a = α, b = β, c = θ, e = ε, dt = ∆t, получаем следующий алгоритм: function [p, m, g, s] = EstimateGBSP(P, dt) N = length(P) - 1; X = log(P); t = dt*(1 : N)'; [k, ~, E] = regress(X(2 : N + 1), [ones(N, 1), X(1 : N ), t]); a = k(1); b = k(2); c = k(3); e = (E'*E/(N - 3))^0.5; p = exp(a/(1 - b) - c*b/(1 - b)^2*dt); g = -log(b)/dt; s = e*(-2*log(b)/(1 - b^2)/dt)^0.5; m = c/(1 - b) + s^2/2; Функция regress() возвращает значения коэффициентов линейной регрессии в векторе k и ее остатки в векторе E. Также она выдает 95% доверительные интервалы для параметров, но поскольку они в данном случае не требуются, поставлен знак пропуска ~. Функция ones(N, 1) создает вектор единиц нужной длины, необходимый для оценки α. N - 3 - количество степеней свободы для расчета остаточной дисперсии. Поскольку в данном случае используется три объясняющие переменные, из объема выборки вычитается именно это число. Используя функцию SimulateGBSP(), можно проверить эффективность работы EstimateGBSP() на искусственно порожденных данных. Например, ниже можно увидеть гистограммы разброса значений параметров для 1000 реализаций ОПБШ симулированных при помощи SimulateGBSP(100, 100, 0.2, 2, 0.3, 10, 1/250, 1000), что примерно соответствует 10 годам дневных ценовых данных. Можно отметить, что оценки несмещенные (кроме, быть может, γ), поскольку в основном концентрированны вокруг истинных значений, как и должно быть для МНК. Однако дисперсия оценок очень высока для γ и P, что может порождать определенные проблемы на практике. Также интересным тестом является трудный случай, когда начальное значение P0 сильно отклоняется от среднего ценового уровня, задаваемого параметром P в модели бокового движения. В этом случае визуально отличить возврат к постоянному уровню от движения по возрастающей тенденции на коротком горизонте бывает непросто. Однако, как показывают результаты испытаний, обычный МНК неплохо справляется с этой задачей. Поскольку фактор роста процесса равен (μ - ½σ2)T, для создания боковой динамики нужно использовать μ = ½σ2. Например, SimulateGBSP(50, 100, 0.3^2/2, 1, 0.3, 4, 1/500, 1000) выдала фактор роста усредненный по всем траекториям 8%. Это, конечно, хуже чем реальные 0%, но значительно лучше наивной оценки временной тенденции изолированно - более 18%. годовых. По крайней мере, это говорит о том, что МНК в принципе способен различать данные варианты динамики. Таким образом, можно констатировать, что параметры обобщенного процесса Блэка-Шоулза легко идентифицируются в рамках регрессионного подхода, правда, качество оценок может быть низким. Это делает актуальным поиски более устойчивых методов (возможно что-то в духе техник resampling и т.п.). Также интересно было бы измерить эффективность метода максимального правдоподобия, но это уже тема для отдельного исследования. |

 Вход |
Вход | Регистрация
Регистрация


























 О проекте
О проекте Правовая информация
Правовая информация Напишите нам
Напишите нам Карта сайта
Карта сайта Новости
Новости Статьи
Статьи Рынки
Рынки Калькуляторы
Калькуляторы Софт
Софт Архив котировок
Архив котировок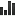 Индикаторы
Индикаторы Библиотека
Библиотека Словарь
Словарь Форум
Форум
Комментарии
q-trader
Руслан
EVVA
Харита
q-trader